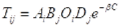
We demonstrate here how MX may be used to run a basic doubly constrained trip distribution model of the form:
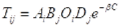
where Ai and Bj are row and column balancing constraints to satisfy the row and column totals Oi and Dj.
It requires as input a skimmed cost matrix ufm file, say input as the first matrix file plus (optionally but most conveniently) an existing trip matrix as the second file; the latter is used below as a convenient method of obtaining the trip ends Oi and Dj.
Thus first create the cost matrix Cij as the internal matrix (which it will automatically become if the first input .ufm matrix is the cost file). Then transform it into the negative exponential (assuming β = 0.01) via the matrix manipulation equation (see 10.8.1).
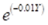
Next enter the matrix factoring option and choose, first, option 3 to factor all rows by factors you select to be the row totals (i.e. origins Oi) from the trip matrix ufm file; see 10.7.4. Thus the internal matrix now becomes:
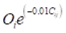
Repeat with option 4 to factor all columns by the column totals Dj to give:
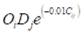
Alternatively, and probably more conveniently, the above three steps could be reduced to a single step via the FORTRAN equation:
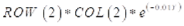
assuming as above that the input trip matrix is the second .ufm file.
Finally choose the matrix Furnessing (10.7.5) and set the trip ends again from the second .ufm input file. Requesting the doubly constrained Furness option solves the original equations.
Goodness of fit statistics comparing the distributed trip matrix (the internal matrix Y) to the assumed observed trip matrix (X2) may be obtained under the Statistics Option and a calibration exercise carried out by trial and error.